作品信息
作品名称:常州旭辉都会里亲子活动中心
Slogan:
建筑轻盈地漂浮于大地,半透明的界面如氤氲的云雾,若隐若现。
企业简介:
日清设计,2001年成立于上海,始终秉承“删繁就简,溯本清源”的建筑哲学,创始人宋照青以la cime(法语“高峰”之意)命名公司,立足本土并以创造一流建筑为目标。经过十多年的发展,公司已拥有700余名建筑师及丰富的国内外大型项目设计经验,并在国内积累了众多住宅、商业、文化、旅游建成项目及高端客户。希望通过培养中国本土化人才和整合精英设计团队,创造出真正符合地域环境的建筑。
作品展示


常州旭辉都会里亲子活动中心
THE METROPOLIS Activity Center
中国,常州
Changzhou, China
建筑以一种轻盈的姿态漂浮于大地,半透明的界面如氤氲的云雾,若隐若现。


©何炼
都会里亲子活动中心位于常州天宁区市机关幼儿园旁,为周边的儿童及家长提供一处温馨的陪伴场所。

©何炼
开启的盒子
_
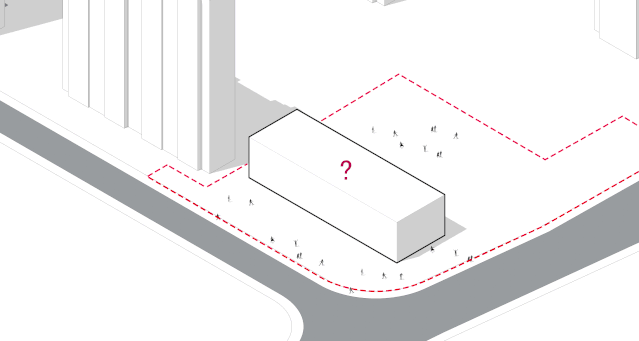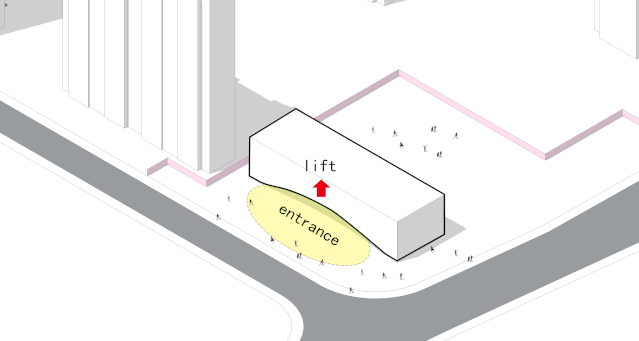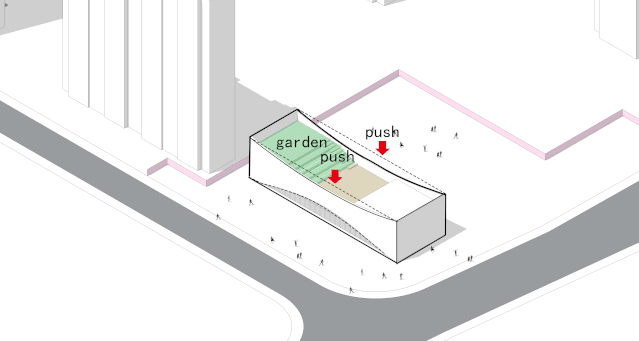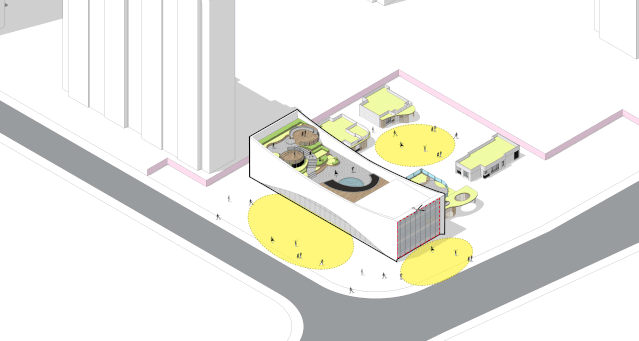
◎体块生成
主体长边沿云桂路横向展开确立出建筑的主要朝向,向南面对城市,向北面对社区,前后两块场地被定义为前广场与后花园。

©何炼
将体量中部从地面轻轻掀起,底部逐渐显露出来,与广场形成连续的公共空间,内外彼此渗透,从城市到广场再到大厅,场所的公共属性从室外进入到室内。
底层开放给大地的同时,屋面也开放给了天空,逐级而上的看台与露天舞台组成了天空花园剧场。东侧山墙面朝曙兴路打开,界定出东侧小广场。


©旭辉江苏区域集团
连续的内外
_
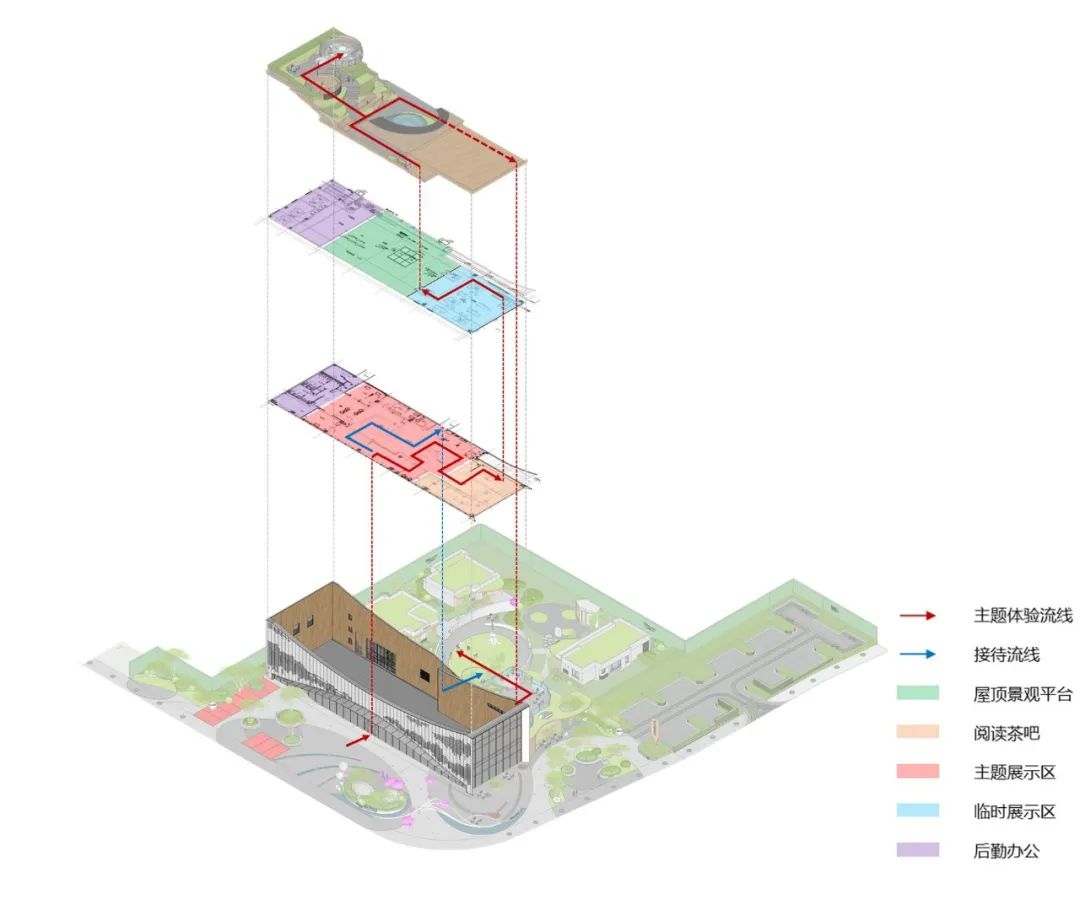
◎流线分析图
首层为主题体验空间,包括阅读书吧,儿童游戏区等情境体验,接待与展示功能并置其中。东西两侧各有一处二层空间,东侧为临时展厅,西侧为办公后勤使用。
天空花园
_


©旭辉江苏区域集团
屋顶是一个朝天空开放的空中花园,为活动中心提供一处安静的休憩场所也为城市提供一处集体生活的舞台,以露天派对等公共活动建立起与城市的亲密连接。
多层幕墙结构体系
_
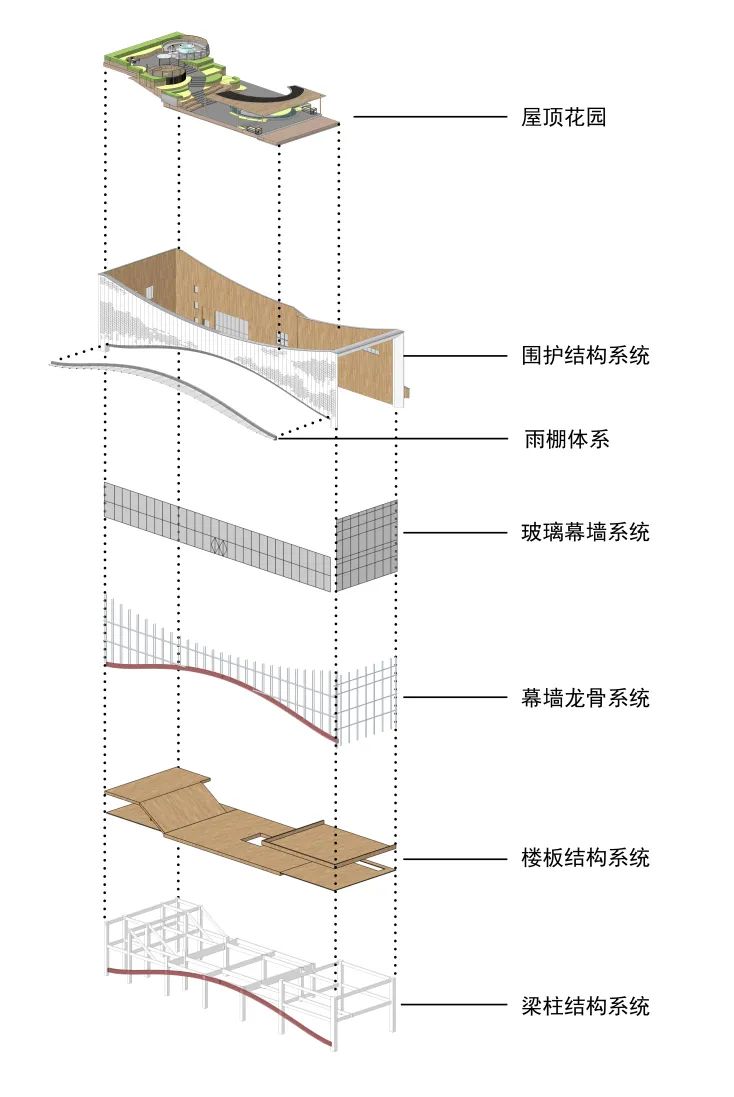
◎结构爆炸分析图
关于建筑围护结构的讨论可以追溯到19世纪建筑师森佩尔提出的建筑四要素理论,即围合(enclosing),遮蔽(roofing),火炉(hearth)和高台(terrace)是构成建筑的四个基本要素。

©何炼
森佩尔认为空间的围护最早是由编织物做成,墙体被看作一种织造物,这与服装之于身体的意义相似,建筑立面一方面承担着围护建筑空间的功能,同时本源地具备了装饰的含义。

©何炼

©旭辉江苏区域集团
主体结构采用框架体系,维护结构采用玻璃+铝板幕墙体系,维护结构通过弧形钢梁与主体框架连接。
界面的多孔与透明
_
孔洞,这种普遍存在于自然万物的形态结构,比如“瘦、皱、露、透”的太湖石,蜂窝密集的巢穴,一片树叶在显微镜下布满着的气孔。
物质世界存在的多孔结构,被哲学家理解为物质之间的关联性,黑格尔认为事物间存在无所不在的渗透,构成“物”的质料不是独立存在的,“多孔性”是彼此之间相互渗透的关系,是构成物质多孔的本质。这一理论也被本雅明、霍尔等引入城市和建筑领域,影响着当代城市建筑的发展。
在主体结构外部包裹着由穿孔铝板构成的表皮。孔隙排列成粒子化的云纹,传递轻盈通透的立面意象,也契合亲子温馨的主题。

◎穿孔板

©旭辉江苏区域集团
孔洞大小和排列的变化,显露出立面丰富的表情。白天阳光和气候的细微变化都会在建筑的立面上产生光影变幻,夜晚建筑也通过孔隙间的泛光向外传达着情绪。
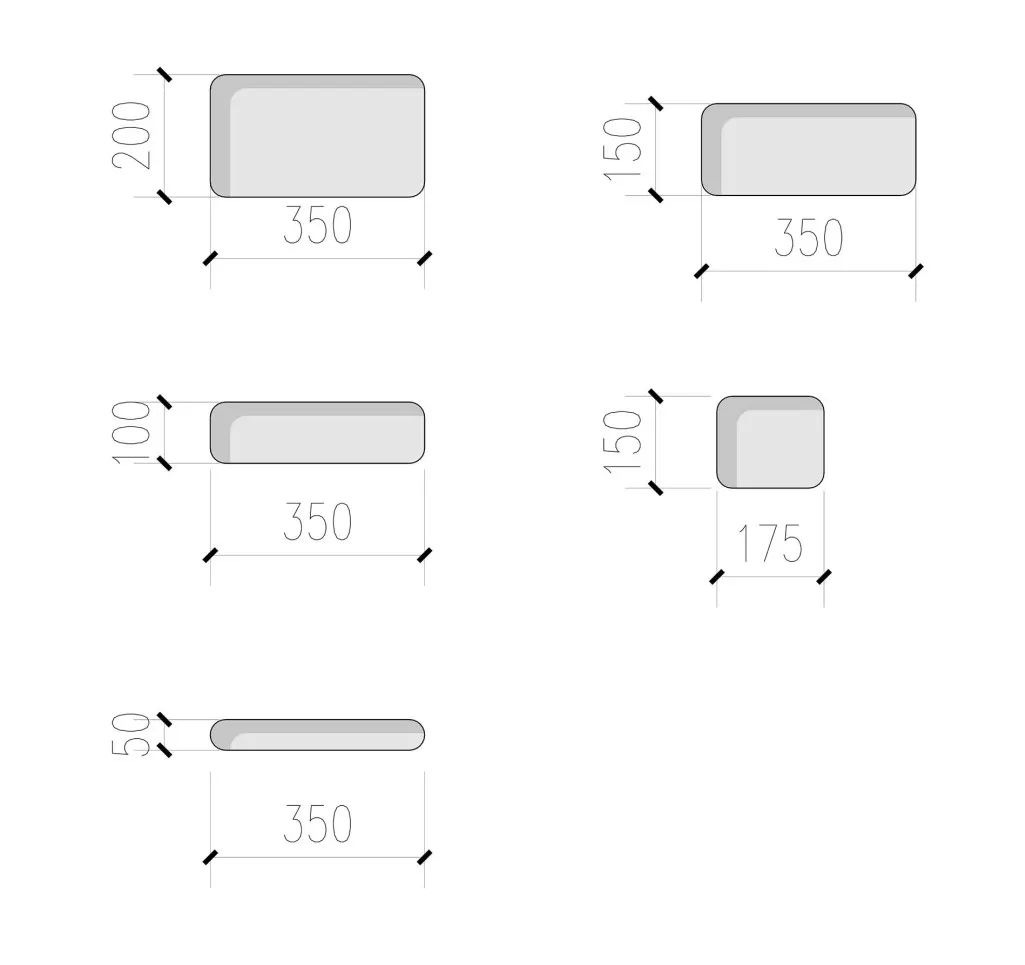
◎穿孔规格

©何炼
靠近底层展示空间的孔隙密度相对较高,开孔尺寸也更大,而上部的孔隙相对稀疏,立面孔隙的密度与开合程度受到室内功能空间的关联影响,这种关联建立了外部立面与内部功能的透明关系。


©旭辉江苏区域集团
穿孔铝板每个开孔四角都处理为圆形倒角,以增强肌理图案的整体性。
会呼吸的皮肤
_
穿孔铝板到内侧墙体之间留有600mm的间隙,一方面类似灯箱的腔体让泛光呈现出更好的效果。
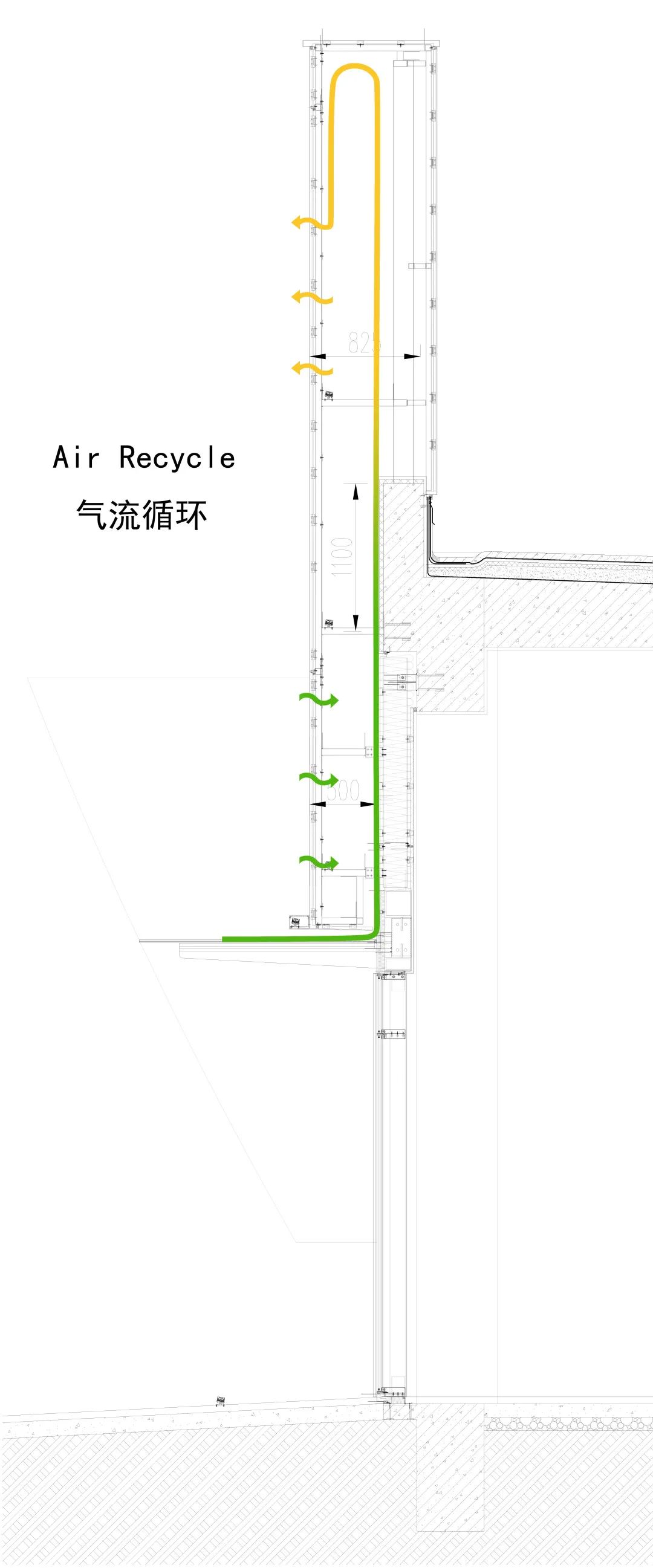
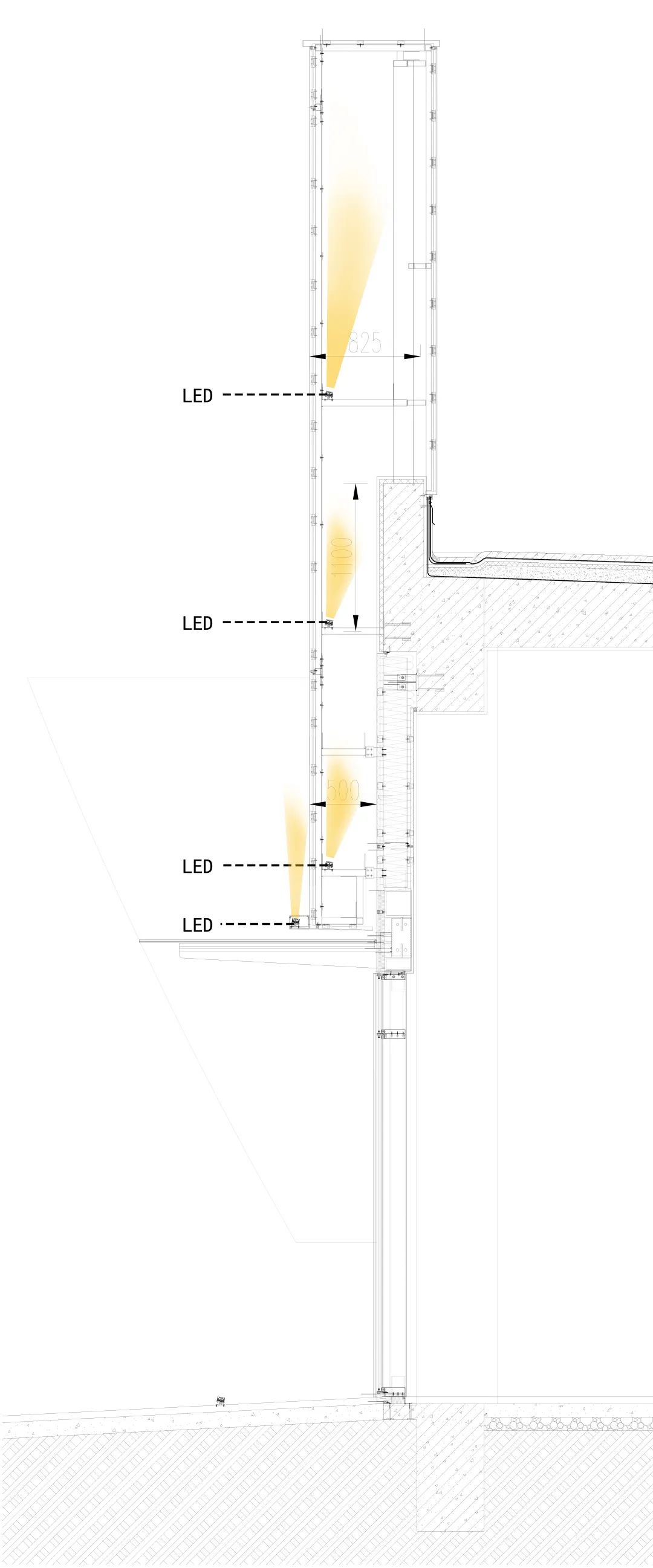
◎双层幕墙空气循环分析图 ◎双层幕墙灯光分析图
另一方面,空腔会隔离室外与室内的热量传导,保温隔热,空腔内部的空气会因温度的差异形成“烟囱效应”,对流循环,通过孔隙与外界交换热量,调节建筑温度。
亲子活动
_

©旭辉江苏区域集团
广场东侧开辟出一块供儿童玩耍的活动场地,孩子们在这里飞舞奔驰尽情地释放天性。

◎儿童天地


©旭辉江苏区域集团
室内专为儿童打造游戏玩耍的场景,孩子们在这里自由地发挥他们的创造力和想象力,家长与孩子地互动让整个中心都充满活力。


◎阅读书吧

©旭辉江苏区域集团
室内楼梯所在的角落被打造成一个温馨的阅读区,空间被整面书架包围,家长与孩子坐在里面畅游知识的海洋分享阅读的乐趣,沿着书墙拾级上至二层展厅。

©旭辉江苏区域集团
二层为儿童和家长提供了一处安静的亲子展厅,定期展出一些孩子们的艺术创作,展厅面对屋顶花园,明亮柔和的光线沿着温暖的木质台阶洒入室内。

©旭辉江苏区域集团
技术图纸
_
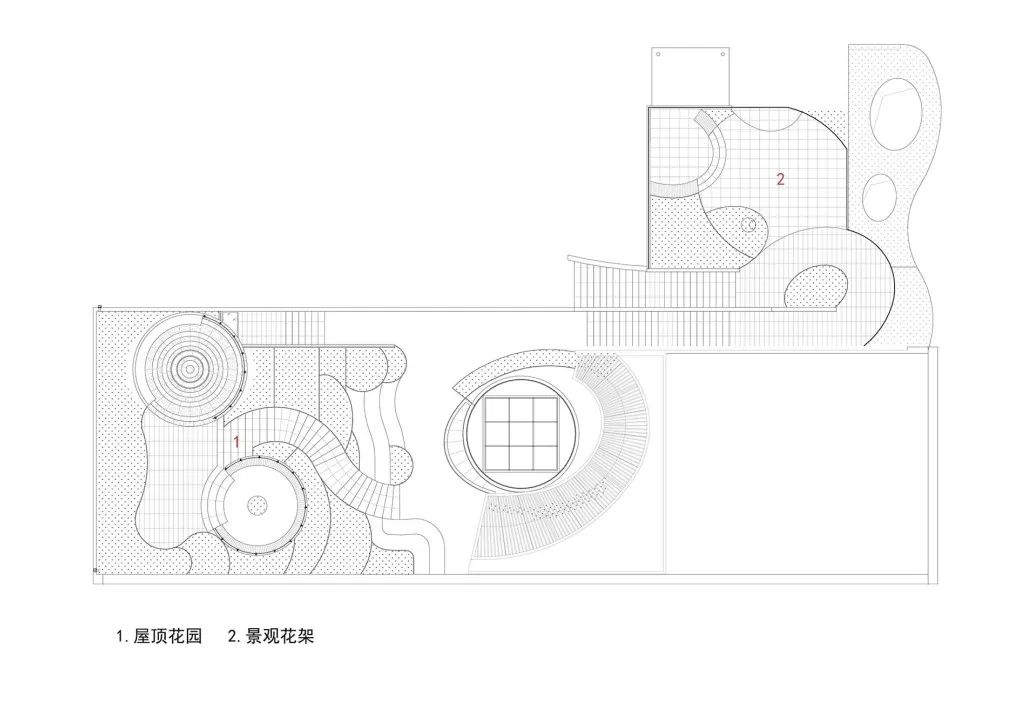
◎屋顶平面图
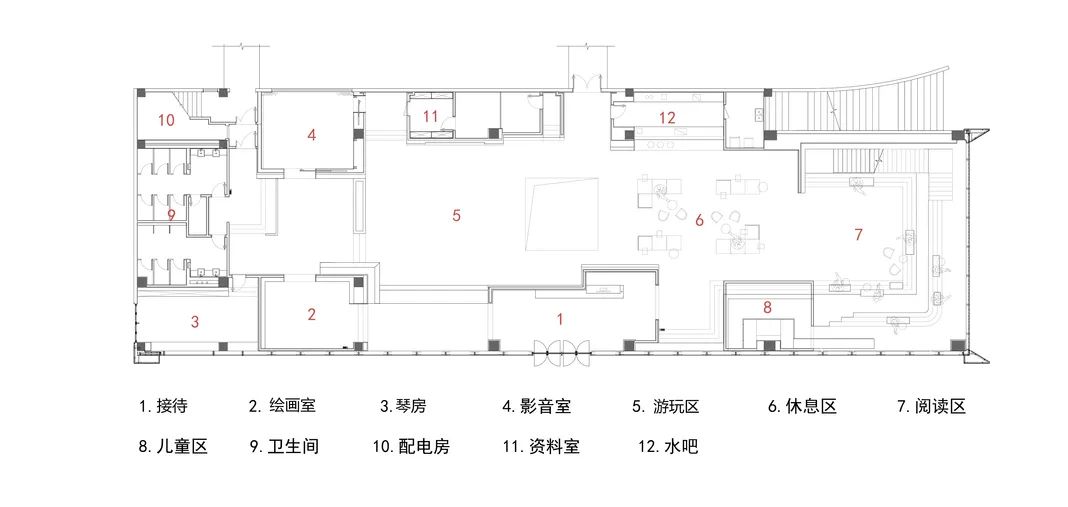
◎一层平面图
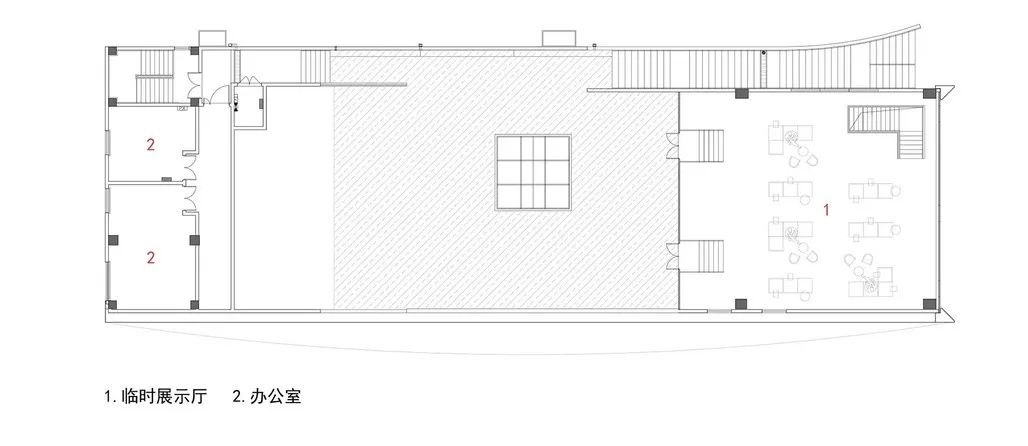
◎二层平面图
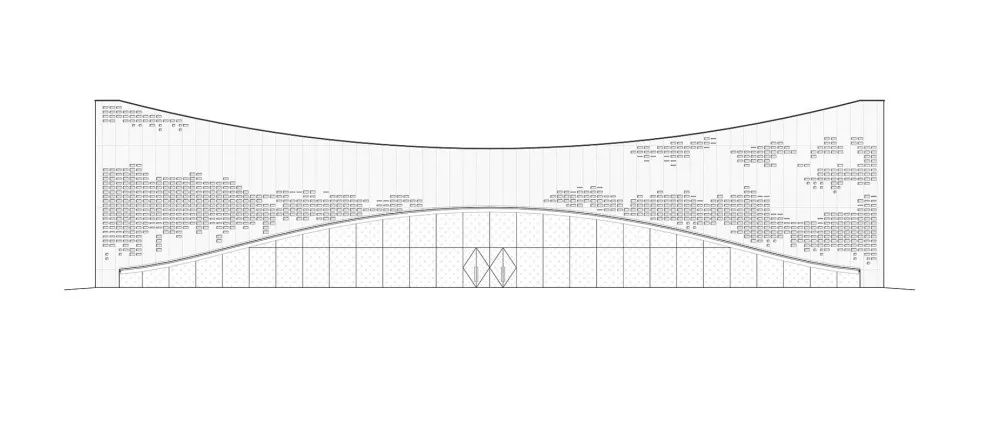
◎南立面图
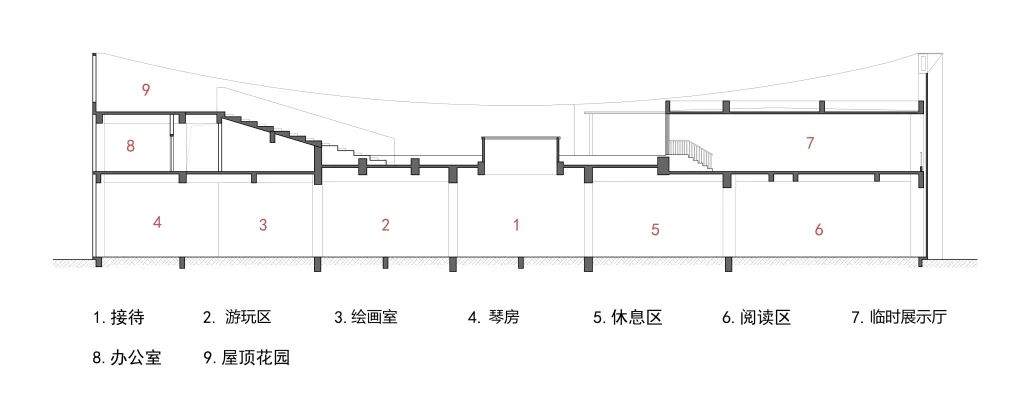
◎剖面图







